[Author note: This post has been edited to correct errors and reduce fluff.]
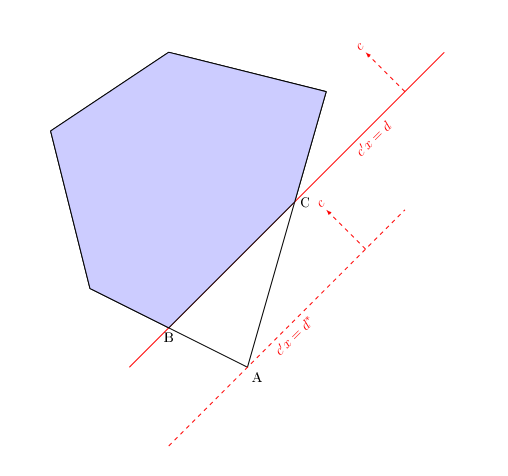
From time to time someone will mention the notion of adding an explicit constraint on the objective value of a mixed-integer programming (MIP) model to the model. If the original model can be written (without loss of generality) as\[
\begin{array}{lrclr}
\mathrm{minimize} & c'x\\
\mathrm{s.t.} & Ax & \ge & b\\
& x & \ge & 0\\
& x_{i} & \in & \mathbb{Z} & (i\in I)
\end{array}
\](where $\mathbb{Z}$ is the set of integers), then the modified model is either\[
\begin{array}{lrclr}
\mathrm{minimize} & c'x\\
\mathrm{s.t.} & Ax & \ge & b\\
& c'x & \ge & d\\
& x & \ge & 0\\
& x_{i} & \in & \mathbb{Z} & (i\in I)
\end{array}
\]if the user seeks to impose a lower bound on the objective value or\[
\begin{array}{lrclr}
\mathrm{minimize} & c'x\\
\mathrm{s.t.} & Ax & \ge & b\\
& -c'x & \ge & -d\\
& x & \ge & 0\\
& x_{i} & \in & \mathbb{Z} & (i\in I)
\end{array}
\]if the user seeks to impose an upper bound on the objective value. Imposing a lower bound may serve to tighten bounds in the LP relaxation a bit; imposing an upper bound may allow for earlier pruning of portions of the search tree (much as supplying a good starting solution would, but without the starting solution and with the danger that too aggressive a bound might cause the solver to conclude incorrectly that the problem was infeasible).
There are two relatively obvious and possibly minor disadvantages to adding the objective constraint explicitly. First, it increases the number of rows in the constraint matrix by one, and thus adds a bit of drag to pivoting operations and a bit of extra memory consumption. Second, the added constraint may raise the density of the constraint matrix, which again creates computational drag. In large scale models, it is not uncommon for the constraints to be sparse -- indeed, they may have to be sparse if you are to solve the model -- but the objective function to be relatively dense. A dense objective function generally creates less computational drag than a dense constraint does.
A possibly more serious issue, though, is a bit less obvious. I first came across it on a support forum, so the ideas here are by no means original. (I believe I first saw it mentioned by IBM's Tobias Achterberg, but I won't swear to that.) Let's start with the linear relaxation of the expanded model in the first case (asserting a lower bound). The dual linear program (LP) is\[
\begin{array}{lrcl}
\mathrm{maximize} & b'y+dz\\
\mathrm{s.t.} & A'y+cz & \le & c\\
& y,z & \ge & 0.
\end{array}
\]Suppose that $x=x^*$ is an optimal solution to the primal problem, and let $(y^*,z^*)$ be a corresponding optimal solution to the dual. The critical observation is that
the added constraint can only be useful if it is binding, so we may assume that $$c'x^*=d=b'y^*+dz^*.$$The impact of this will be that the added constraint
creates either dual degeneracy or an infinite number of optimal solutions to the dual.
Let me dispense with the most common case first. Suppose that $z^*=1$. It follows that $A'y^*\le 0$ and $b'y^*=0$, in which case $y=\lambda y^*,z=z^*=1$ is optimal in the dual for any $\lambda \ge 0$. So there are infinitely many solutions to the dual (in fact, an entire ray) unless $y=0$ (which is actually the most likely scenario), in which case the dual solution is massively degenerate. I illustrate this in my
next post.
The remaining cases are "edge cases" (no pun intended), corresponding to the added constraint being tangent to the original feasible region (making the primal solution degenerate). I will grind through the algebra below, but feel free to skip it, as it is not clear that the added constraint will be tangent to the feasible region often enough to worry about.
Now assume that $z^*\lt 1$. Let $z=z^* + \epsilon$ and $$y=\left(1-\frac{\epsilon}{1-z^*}\right)y^*$$for an arbitrary $\epsilon$ with $0\lt \epsilon \le 1-z^*$. We verify easily that $y\ge 0$,$$\begin{gather*}
A'y+cz=\left(1-\frac{\epsilon}{1-z^{*}}\right)A'y^{*}+\left(z^{*}+\epsilon\right)c\\
\le\left(1-\frac{\epsilon}{1-z^{*}}\right)\left(c-z^{*}c\right)+\left(z^{*}+\epsilon\right)c\\
\le\left(1-\frac{\epsilon}{1-z^{*}}\right)\left(1-z^{*}\right)c+\left(z^{*}+\epsilon\right)c\\
=\left(1-z^{*}-\epsilon\right)c+\left(z^{*}+\epsilon\right)c\\
=c,
\end{gather*}$$and $$\begin{gather*}
b'y+dz=\left(1-\frac{\epsilon}{1-z^{*}}\right)b'y^{*}+d\left(z^{*}+\epsilon\right)\\
=\left(1-\frac{\epsilon}{1-z^{*}}\right)\left(d-dz^{*}\right)+dz^{*}+d\epsilon\\
=d-dz^{*}-d\epsilon+dz^{*}+d\epsilon\\
=d.
\end{gather*}$$So $(y,z)$ is another optimal dual solution for any $\epsilon\in (0,1-z^*)$, and we again have an infinite number of optimal solutions to the dual.
Finally, the case $z^*\gt 1$ is similar (and similarly tedious). Set $z=z^*-\epsilon$ where $0\lt \epsilon\lt z^*-1$ and set$$y=\left(1-\frac{\epsilon}{z^*-1}\right)y^*.$$Verification that $(y,z)$ is feasible in the dual and that $b'y+dz=d$ is left to the reader as an annoying exercise.
It turns out that adding an upper bound on the objective (lower bound in a maximization) is less likely to be problematic (as I discuss/hand-wave in my
next post). The extra constraint still does add drag, and if it happens to be tangent to the feasible region, we can again encounter multiple dual solutions and/or dual degeneracy.
Why do we care that the dual has an infinite number of solutions? The dual solution comes into play in a number of ways when solving a MIP model, from pricing primal columns to fixing primal integer variables and other node presolve reductions. While there is no guarantee that having an infinite number of dual solutions will slow the algorithm, and in fact that is always possible even without constraining the original objective, it is reasonable to suspect that making the dual information at a node less precise is unlikely to help and plausibly likely to hurt ... a suspicion that I believe has been born out in practice.
There are alternatives to imposing constraints on the objective value. One is to change the objective to minimization of a new variable $w$ and add the constraint $c'x-w=0$ (or $c'x-w\le 0$, which is equivalent). You are still expanding the problem and possibly increasing the density of the constraint matrix, but I believe this will avoid the problem of introducing an infinite number of dual solutions.
CPLEX has parameters CutUp and CutLo that allow you to impose an upper limit on the objective of a minimization problem and a lower limit on the objective of a maximization problem respectively. This gets you the potential earlier pruning of the search tree without introducing multiple dual solutions. I suspect that other solvers provide something similar.
Update: For a discussion of this topic, including why the use of $w$ may still create issues, see
Tobias Achterberg's reply in
this thread on the CPLEX support forum.